数组
本文为学习代码随想录时所做的笔记,仅供学习参考,不做任何商业用途,若有侵权,请联系删除。
数组
二分查找
704. 二分查找 - 力扣(LeetCode)
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
1 | |
思路
二分法应当注意对区间的定义。区间的定义就是不变量,要在二分查找的过程中,保持不变量,就是在while寻找每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
二分法区间的定义一般为两种,左闭右闭 [left, right],或者左闭右开 [left, right)。
[left, right]
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};[left, right)
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
相关题目
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
移除元素
27. 移除元素 - 力扣(LeetCode)
思路
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
- 快指针:寻找新数组的元素,新数组就是不含有目标元素的数组
- 慢指针:指向更新新数组下标的位置
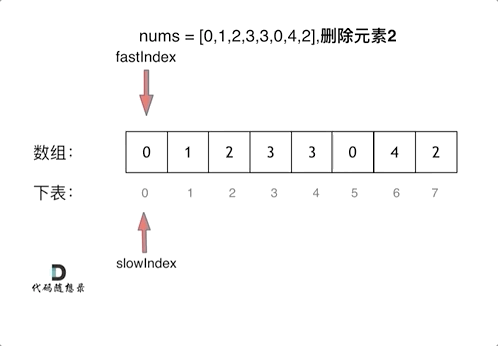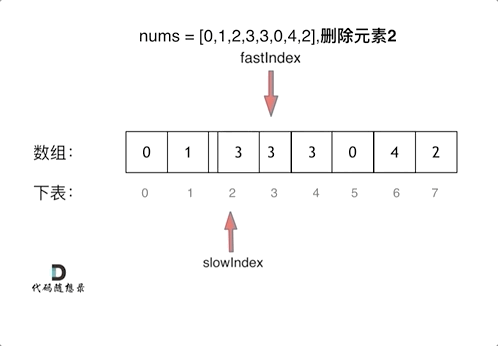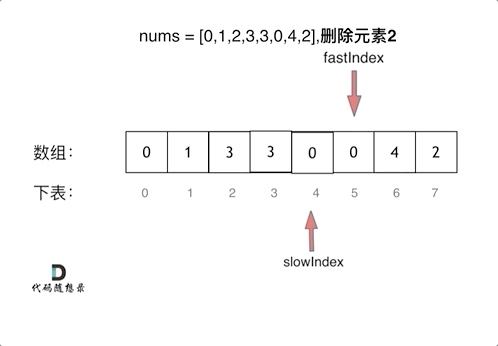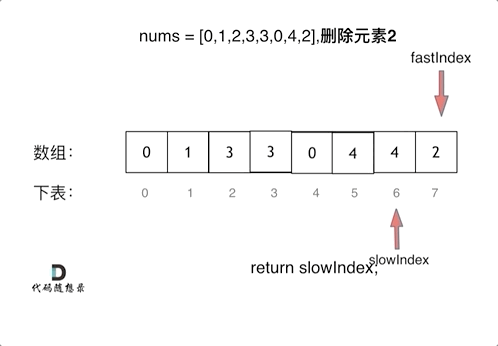
1 | |
相关题目推荐
26. 删除有序数组中的重复项 - 力扣(LeetCode)
1 | |
1 | |
一个字符是否会被删掉,只取决于该字符后面的退格符,而与该字符前面的退格符无关。因此当我们逆序地遍历字符串,就可以立即确定当前字符是否会被删掉。
一个字符是否会被删掉,只取决于该字符后面的退格符,而与该字符前面的退格符无关。因此当我们逆序地遍历字符串,就可以立即确定当前字符是否会被删掉。
具体地,我们定义skip 表示当前待删除的字符的数量。每次我们遍历到一个字符:
若该字符为退格符,则我们需要多删除一个普通字符,我们让skip加 11;
若该字符为普通字符:
若 skip 为 0,则说明当前字符不需要删去;
若 skip 不为 0,则说明当前字符需要删去,我们让 skip 减 11。
这样,我们定义两个指针,分别指向两字符串的末尾。每次我们让两指针逆序地遍历两字符串,直到两字符串能够各自确定一个字符,然后将这两个字符进行比较。重复这一过程直到找到的两个字符不相等,或遍历完字符串为止。
作者:LeetCode-Solution 链接:https://leetcode.cn/problems/backspace-string-compare/solution/bi-jiao-han-tui-ge-de-zi-fu-chuan-by-leetcode-solu/ 来源:力扣(LeetCode)
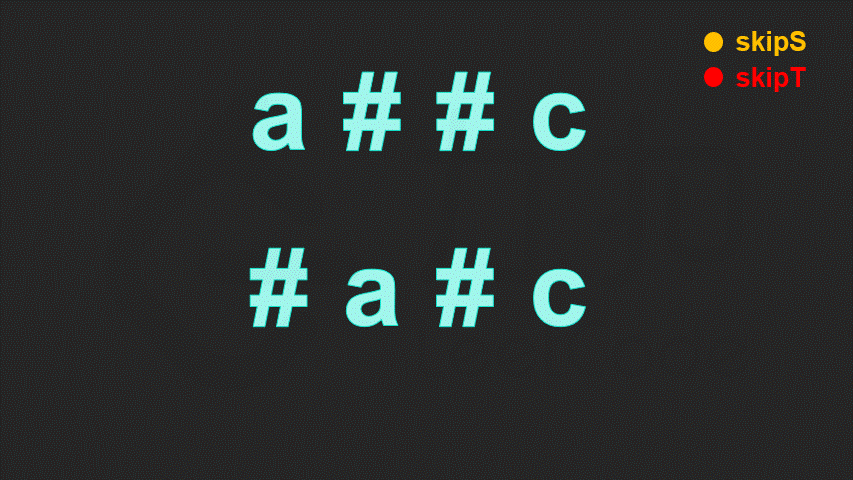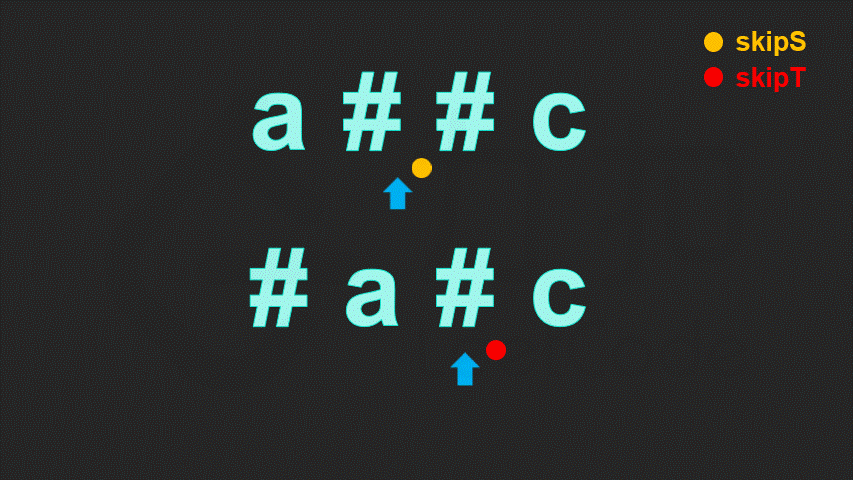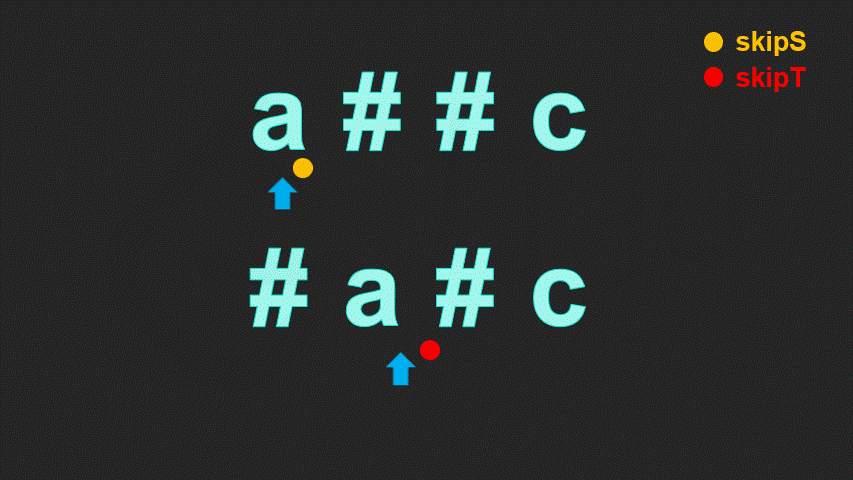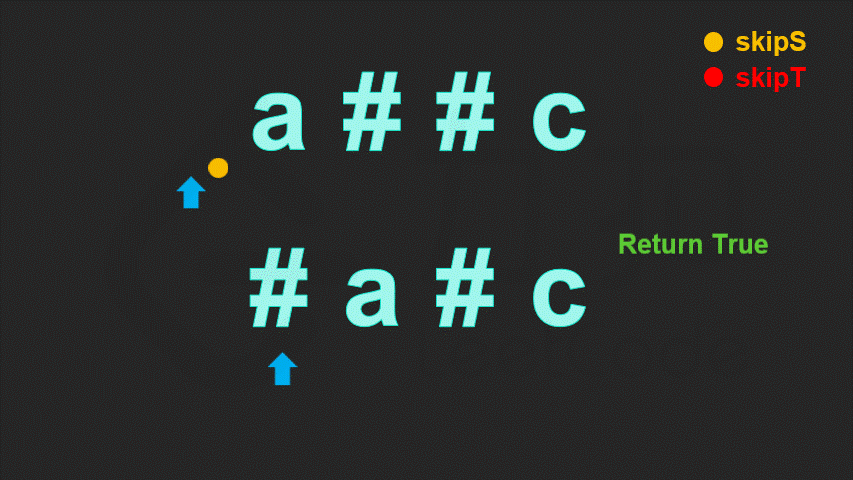
1 | |
1 | |
滑动窗口
209. 长度最小的子数组 - 力扣(LeetCode)
思路
所谓滑动窗口,就是不断地调节子序列的起始位置和终止位置,从而得出我们想要的结果。
在本题内实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,窗口的起始位置设置为数组的起始位置就可以了。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
1 | |
相关题目推荐
1 | |
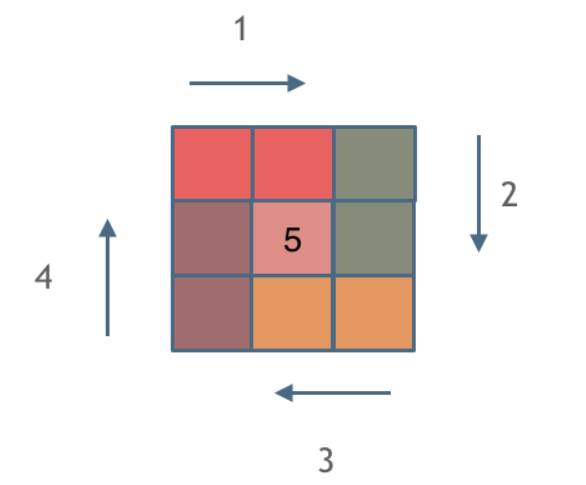
螺旋矩阵
59. 螺旋矩阵 II - 力扣(LeetCode)
思路
循环不变量原则
边界条件很多,应当按照固定规则来遍历
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
1 | |